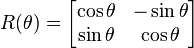The invariance of moments in Virtual 2D space

Image Moments

A moment is an abstract concept used as a quantitative measure of a set of points. In physics, if the points represent mass, the zeroth moment refer to the total mass. Higher moments are also used to derive other important measurements, such as  the center of mass (first moment divided by the total mass) and rotational inertia (second moment).

Under certain conditions these moments are invariant to changes in coordinates, scaling, and orientation. In the case of the center of mass, moving all the points to a new location, will not change its value, provided their relative locations (with respect to the origin) are maintained. Another example: in geometry, a circle (on the x-y Cartesian plane) will not increase or decrease in size, provided the relation (x-x_o)² + (y-y_o)² = R² is maintained. (x_o,y_o) refers to the new origin.

A similar set of quantities are used can be used to analyze shapes and images.

For a gray scale image I(x,y), its moments are defined as

Each point in the image is weighted using it's gray level value I(x,y), coordinates (x,y) and  i, j. M₀₀ is analogous to the total mass of the image. For a binary images consisting only of 0 and 1 values, it is analogous to the area. Notice that the black background I(x,y) = 0 does not contribute to M_ij.

In its current form, this is not invariant to changes in location. In this case, we can derive central moments using M₀₀.

with

 

Finally, for changes in scale, these are the scale-invariant moments

for i + j >= 2

Hu derived a set of invariant moments that can be used in visual pattern recognition

where I₁ is analogous to the moment of inertia. I₇ is the skew operator can be used to identify mirror images. The full set provides a handy way of determining whether any two images are identical or just mirrored versions of one another. Because it is invariant due to rotation, no further transformations are needed to facilitate the identification process. One can simply take a snapshot of the region of interest, subtract the background, and compute the corresponding image moments and compare it to known measurements. This also bodes well for software automation. Finally, due to scale invariance, theoretically, all distinct properties of the image can be observed regardless of the size of the sample. A practical application of this is when you maintain an image database, you need not store multiple versions of the image taken at different magnifications and/or camera zoom levels.

We performed numerical experiments on three types of images: grey scale image, synthetic image, and an edge image of a real object.

Grayscale image

original

flipped

scale (x 2.0)

rotated (90 degrees)

translated

Invariant Moments

	original	flipped	scaled (x 2.0)	rotated (90o)	translated
I1	9.895305	9.895305	9.895385	9.895305	9.895305
I2	1.401796	1.401796	1.401796	1.401796	1.401796
I3	1.212552	1.212552	1.212552	1.212552	1.212552
I4	3.686399	3.686399	3.686399	3.686399	3.686399
I5	2.404242	2.404242	2.404242	2.404242	2.404242
I6	4.351743	4.351743	4.351743	4.351743	4.351743
I7	-5.422867	5.422867	-5.422867	-5.422867	-5.422867

In all of the moments, are all invariant under translation, scaling and rotation. For the flipped image (horizontal), the changing sign of the I₇ indicates the flipped image. Under scaling and translation, there is no significant change in the values.

Synthetic binary edge image

original

flipped

scale (x 2.0)

rotated (90 degrees)

translated (to 52,52)

Invariant moments

	original	flipped vertically	scaled (x 2.0)	rotated (90o)	translated
I1	6.353301	6.353353	6.353817	6.353301	6.353301
I2	4.345424	4.347722	4.345424	4.345424	4.345424
I3	2.405847	2.400483	2.405847	2.405847	2.405847
I4	8.438474	8.431695	8.438474	8.438474	8.438474
I5	1.202347	1.199559	1.202347	1.202347	1.202347
I6	5.562628	5.559628	5.562628	5.562628	5.562628
I7	-5.926998E-21	5.402808E-7	-1.327250E-20	0.000000	-3.806771E-21

For the synthetic case, only the skew operator shows much variance and I₄ for the flipped image. A work by Flusser and Suk demonstrated that some of the image moments by Hu are not completely independent. They have derived a new set. We have tested this synthetic image against Flusser's set as show below

Flusser-Suk rotationally  invariant moments

	original	flipped	scaled (x 2.0)	rotated (90o)	translated
I1	6.353425	6.353477	6.353942	6.353425	6.356209
I2	24.361843	24.51292	24.358246	24.361843	238.111670
I3	-160.562535	-161.6012	-160.538824	-160.562535	868.962119
I4	0.000000	0.03786704	0.000000	0.000000	-1304.758197
I5	-1781.199425	-1796.049	-1780.804879	-1781.199425	-46188.231920
I6	0.000000	0.9120794	0.000000	0.000000	-11545.862316

To some degree, the rotated image is nearly identical to the original in Flusser's moments. At this moment, I observe the large deviations on the translated and flipped versions. Could it be that Flusser's moments are not translation invariant? Need to verify this.

Edge image (chromosome)

original

flipped

scale (x 2.0)

rotated ( -90 degrees)

translated

Invariant moments

	original	flipped	scaled (x 2.0)	rotated (-90o)	translated
I1	3.15595718	3.15595718	3.15699884	3.15595718	3.15595718
I2	5.07844102	5.07844102	5.07844102	5.07844102	5.07844102
I3	0.79003543	0.79003543	0.79003543	0.79003543	0.79003543
I4	0.25408407	0.25408407	0.25408407	0.25408407	0.25408407
I5	0.11280773	0.11280773	0.11280773	0.11280773	0.11280773
I6	0.35999914	0.35999914	0.35999914	0.35999914	0.35999914
I7	-0.01528518	0.01528518	-0.01528518	-0.01528518	-0.01528518

For the edge image of the chromosome from the previous exercise, all values are identical except for the skew operator of the flipped case.

Some thoughts

This has been a challenge to implement. A lot of code-rewrites were done especially on the functions computing for the complex moments.

We've used images in this exercise, but in theory it should also be applicable for shapes or data containing only the vertices of polygons. Operating on shapes meant that rotation operations would not totally result in aliasing or loss of information. One need only guard against number precision (before and after the floating point operations), truncation and other related issues. Overall M₀₀ should remain constant.

I've started coding these at: https://github.com/daelsepara/pixelprocessing/tree/master/Shape. 

References

• Wikipedia contributors, "Image Moment," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Image_moment


• Wikipedia contributors, "Moment (physics)," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Moment_(physics)

• Hu, M.K. (1962) "Visual Pattern Recognition by Moment Invariants", IRE Trans. Info. Theory, vol. IT-8, pp.179–187, 1962

• Flusser, J   "On the Independence of Rotation Moment Invariants", Pattern Recognition, vol. 33, pp. 1405–1410, 2000

• Flusser, J  and Suk, T, "Rotation Moment Invariants for Recognition of Symmetric Objects", IEEE Trans. Image Proc., vol. 15, pp. 3784–3790, 2006


• Fisher B, "2D Binary Image Moment Invariants", http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/FISHER/MOMINV/

• Soriano, M (2015), Moment Invariants, lecture notes presented in Physics 301 - Special Topics in Experimental Physics (Advanced Signal and Image Processing) at National Institute of Physics, University of Philippines Diliman, Quezon City on 11 August 2015

Useful R tips #1

Clear all user-defined objects and functions

rm(list = ls())

This command will clear all functions and objects defined (or in memory). Why would you want to do that? Sometimes, functions and variables may not contain the expected values (or behavior) . As is often the case, they may be sharing a name with another global variable or function previously defined. What may happen spans the  full spectrum of what the hell. You do not need to run this command every time, perhaps only at the start of a new R session.

Normalized Inverse Fast Fourier transform (FFT)

fft(z, inverse = TRUE) / length(z)

Taking the inverse FFT in R has a peculiar side-effect. The results are almost always not normalized. In the last activity, this means that after clipping selected frequencies in the power-spectrum, plotting the descriptor (from the inverse FFT) will not overlap with the original. Normalizing the inverse yields the "expected" result.

R codes now hosted at GitHub

All R codes I have used in our activities are hosted at GitHub: https://github.com/daelsepara/pixelprocessing

Smooth

In the last exercise, it is possible that multiple corners are observed, which may complicate the process of determining the chromosome's major axis. Often, these other "corners" are not of interest. They do not correspond to the ones that are farthest along chromosome's major axis. They are  important details but for now, they may be conveniently ignored in this phase of the classification. What we need is a method that removes these "extra" details, while preserving the overall shape of the chromosome.

Fourier Descriptors

From the Freeman vector code (FVC), we obtain the contour by computing for the locations of all the points along the FVC starting at seed, and then moving along the boundary, in the direction specified by the codes. Once we have the x and y-coordinates of those points, we create a Fourier descriptor for the shape by creating a complex vector from x's and y's: x + iy. Taking the discrete Fourier transform (DFT) of the complex-valued vector produces the shape's Fourier descriptor.

Fourier descriptors have properties inherited from Fourier transforms:

• Translation invariant
• Scale invariant
• Rotation and starting point

Translation invariant means that the Fourier descriptors remain the same no matter where the shape is located. Scaling the shape by a factor also scale the descriptor by the same amount. Finally, changing the origin or the orientation of the shape (through rotation) only affects the phase of the descriptors. (see Wolfram Demo site listed in the reference section)

Smooth operator

Power spectrum

In the figure above, we have an outline of a chromosome showing numerous spikes along its contour line. The power spectrum (log10 scale), show its frequency content. Notice that the power spectrum plot is mirrored and symmetric. Half of the result contain its negative frequencies content. Usually an FFTSHIFT operation is performed so that the plot is centered at f = 0. f = 0 correspond to the bias of the signal. If the contour were translated so that the origin is at (0,0) and its x and y components contains positive and negative values, we see this bias eliminated from the power spectrum.

Now, on to the business of removing the spikes. It turns out that this is straightforward process. Simply clipping, or, removing the higher frequencies by setting them to 0 and taking the inverse Fourier transform removes the spikes, i.e. making the contour smoother.

And if more frequencies are filtered out, it becomes even smoother.

Note

• The Fourier transform works for an infinite, continuous signal. For finite, sampled signals, such as those used in our computations, we use the discrete Fourier transform (DFT). All properties of the Fourier transform also applies to the DFT.

References

• Wikipedia contributors, "Discrete Fourier transform," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Discrete_Fourier_transform


• William Sethares, "Fourier Descriptors", http://demonstrations.wolfram.com/FourierDescriptors/, Wolfram Demonstrations Project, Published: February 21, 2012


• Soriano, M (2015), Fourier Descriptors, lecture notes presented in Physics 301 - Special Topics in Experimental Physics (Advanced Signal and Image Processing) at National Institute of Physics, University of Philippines Diliman, Quezon City on 7 August 2015

Trying Freeman

Feature extraction

Feature extraction is an essential part of image processing and more generally, machine learning. For example, if we were to identify objects found in a picture, we would make a list. This would be a list of objects we recognize in the picture, e.g. clock, person, table, etc. This list would be more compact than the picture: storing it digitally would take lesser space than the multi-mega-pixel picture. This kind of data boosts image search engines because the list would serve as the meta data associated with the image. Instead of analyzing each pixel in a large number of images, the system may search the meta data instead and return all that satisfy the search parameters.

In the above example, we have done feature extraction. Recognition (by whatever means our minds used) is the extraction part and the objects are the features. Object recognition is a straightforward, albeit tedious process for humans. To automate this, we employ algorithms. One of many ways in which we perform object recognition is by analyzing shapes. Regular shapes such as circle, square, rectangle, are easy to describe because they have well-defined geometries. For circles, we need only to specify an origin and a radius.  For squares, rectangles and other parallelograms, we only need to determine the location of its four vertices. But what about arbitrarily-shaped objects or objects with ill-defined geometries?

Freeman vector code

Freeman vector code (FVC) is a simple and compact method of encoding arbitrary geometric configurations. We begin with the boundaries of the object of interest. The boundaries may or may not form a close loop. We choose a starting point (seed) then assign discrete values to pinpoint the location of the next point along the boundary. This is performed repeatedly until we reach the end of the boundary. For shapes, the terminating condition occurs when we have reached the starting point, i.e. the loop is closed.

In a digital image, each pixel has 8 surrounding neighbors. Location of the next pixel is specified by assigning discrete values from 1-8. The search for the location of the next pixel proceeds clockwise, i.e. search in the upper-left neighbor proceeds first before searching in the location directly above the seed, and so on. The next location becomes the new seed. These steps are repeated until the terminating condition is satisfied. This will effectively produce a vector. Because they are vectors, we can translate them, i.e. render them in another location just by plotting a pixel in the direction specified by its elements.

For further analysis, the curvatures of the shape are informative. These are obtained from the gradients (difference of two adjacent vectors) and running sums of three adjacent gradients. (More comments on gradients and running sums later)

Freeman vector code algorithm
From: J.A.F. Balista et al. / Pattern Recognition Letters 31 (2010) 20–27

Prelude to chromosome classification

In this exercise we applied Freeman vector coding in analyzing a single chromosome pair. We begin with an image of a single chromosome pair. We first perform edge detection using a Sobel filter to produce the image on the right in the picture below

The resulting outline is thick. We can further tweak the intensity threshold or we can use a different filter. In our experiment we only used the outer boundary. We chose a pixel on the outer boundary as a starting point (x,y) = (2,49) and obtained the Freeman-vector code. A common problem we have encountered was when the algorithm failed to obtain the correct shape: algorithm did not terminate at the seed or a different shape is obtained. Even with the neighborhood search proceeding clockwise, the problem kept occurring.

Our solution was to incorporate a form of simple "memory" to the algorithm. This involved "remembering" and modifying the starting point of the neighborhood search. For pixels with codes 1-4, i.e. top half of the FVC, the search proceeds normally, with the neighborhood search still beginning at 1. For codes 5-8, the starting direction is 5, proceeding clockwise from 5 to 8, then 1 to 4. This can be done by a modulo operation or simply getting the overflow over 8.

Once we have obtained the correct shape, we compute for the gradients and running sums. To get two adjacent vectors, we obtain the difference between the original Freeman vector and the same vector shifted one element to the left. In the same manner, to get the running sum, we obtain the sum of the original gradient and two other, shifted once and twice to the left. 

In the figure above, we obtained the FVC, and computed the gradients and running sum. We have labelled points of interest in all images. Our seed is at point H. It is interesting to note that the gradients indicates the slope of the curve at that point. It indicates the magnitude and direction of the change, i.e. increasing or decreasing. This seems to be the case for all points except C. Intuitively, and by inspection, the gradient should be more positive. What have we done wrong? 

The fault is in our code.

From point B to C, the code is as string of 8's. Then at point C, we see it shifting in the direction of 1, Simply computing the gradient at that point results in a massive 1 - 8 = -7. We should probably modify the code to handle this but for now, we have left it as it is, and just made a mental note of it (likely a very bad practice in reality)

How do we find the chromosome's corners?

In the image of running sum, we see clumps of values (3 consecutive negative or positive values) about some points. At Point B, D, H and I, the cluster of values are positive (convex), including perhaps C, if we handled the case properly. While at points A, E, F, the values are negative (concave). These correspond very well to the corners in the image above. While at point G, there were no clustered values in the running sum, indicating that it is not a corner.

Dancing chromosomes

Two more processes are involved in chromosome classification: segmentation, axis and centromere

location, and classification. While we will not go into more detail about these processes, the location of the corners from the earlier algorithm may help us in this case. We compute for the center of our chromosome by taking the mean of the vertices. Prior to rotation, we translate them about about the origin at (0,0).

Rotation is done using the rotation matrix

This allows us to compute for the new location of the (x,y)

We can use a rotation angle based on the chromosome's axis, or in our case, the midpoint location between the top or bottom corners. In this demonstration, we deliberately chose to rotate it by -45 degrees. Results are shown in the image below. Incidentally, the location of the origin corresponds very well to the likeliest location of the centromere. Above the centromere are the short arms, and the below it are the long arms of the chromosome.

Summary

We have used the Freeman vector code to obtain a vector description of the chromosome's shapes. The gradient and the running sums of the adjacent vectors (generated) from the Freeman vector, allowed us to determine the location of chromosome's corners.

Additional Notes

• All algorithms were coded in R: Freeman vector coding, gradients, running sums, and rotation.

• The algorithm used in the original 1961 paper used the codes 0-7 and ran counter-clockwise. 

• In the figure above of the Freeman vector code algorithm, we have not shown the color intensity patterns. See the paper for the complete image.

References

• H. Freeman (1961) ‘On the encoding of arbitrary geometric configurations’, IRE Trans. on Electronic Computers, 10(2):260-268

• J. Balista, M. Soriano, C. Saloma (2010) ‘Compact time-independent pattern representation of entire human gait cycle for tracking of gait irregularities’, Pattern Recognition Letters 31(1):20-27.

• Wikipedia contributors, "Shape," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Shape

• Wikipedia contributors, "Edge detection," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Edge_detection

• Wikipedia contributors, "Chromosome," Wikipedia, The Free Encyclopedia,https://en.wikipedia.org/wiki/Chromosome

• Soriano, M (2015), Image and Signal Feature Extraction: Shape, lecture notes distributed in Physics 301 - Special Topics in Experimental Physics (Advanced Signal and Image Processing) at National Institute of Physics, University of Philippines Diliman, Quezon City on 4 August 2015.

The Call of Image Processing

Welcome to this blog.

The most beautiful thing in the world, I think, is the ability of the human mind to absorb a lot of content. We are standing on the shores of our little islands facing an infinite sea of possibilities, and it calls us to voyage far. The sciences, each expanding towards new directions have benefited us immensely; yet some day the piecing together of seemingly dissociated knowledge will open up such fantastic vistas of reality, and of our position therein, that we shall either be subdued by the revelation or push on towards the welcoming light, into the excitement and uncertainty of a new golden age

If the above words sound familiar, it is because it is a revision of the nihilistic opening lines of HP Lovecraft's Call of Cthulhu. Unlike the narrator, I am more hopeful and optimistic about man's never ending pursuit of knowledge. We will generate aplenty and it will probably confound us most of the time. Initially, a lot of it may seem disparate or incompatible, but a lot of new discoveries and research are happening on the frontiers of different disciplines: and that is exciting!

In this regard, I am especially intrigued by the things I will be learning and applying from the Advanced Signal and Image Processing course I am taking up this semester. Sure, we have always been processing signals and images. Our online world today is overflowing with signals from various sources, especially from social network feeds. What may have once been the province of computer-folks are now part of many scientists' arsenal. In short, image processing has gone mainstream. As part of the requirements of the course, this blog will be a record of our activities, machine problems, discussions and probably a few digressions.

To end this post, the image below is a result from my earlier local conference paper (2009). I processed the last two images (with the Gerchberg-Saxton algorithm) to generate a bitmap used by the SLM (spatial light modulator) to modify the light pattern used in optical lithography.