Feature extraction
Feature extraction is an essential part of image processing and more generally, machine learning. For example, if we were to identify objects found in a picture, we would make a list. This would be a list of objects we recognize in the picture, e.g. clock, person, table, etc. This list would be more compact than the picture: storing it digitally would take lesser space than the multi-mega-pixel picture. This kind of data boosts image search engines because the list would serve as the meta data associated with the image. Instead of analyzing each pixel in a large number of images, the system may search the meta data instead and return all that satisfy the search parameters.
In the above example, we have done feature extraction. Recognition (by whatever means our minds used) is the extraction part and the objects are the features. Object recognition is a straightforward, albeit tedious process for humans. To automate this, we employ algorithms. One of many ways in which we perform object recognition is by analyzing shapes. Regular shapes such as circle, square, rectangle, are easy to describe because they have well-defined geometries. For circles, we need only to specify an origin and a radius. For squares, rectangles and other parallelograms, we only need to determine the location of its four vertices. But what about arbitrarily-shaped objects or objects with ill-defined geometries?
Freeman vector code
Freeman vector code (FVC) is a simple and compact method of encoding arbitrary geometric configurations. We begin with the boundaries of the object of interest. The boundaries may or may not form a close loop. We choose a starting point (seed) then assign discrete values to pinpoint the location of the next point along the boundary. This is performed repeatedly until we reach the end of the boundary. For shapes, the terminating condition occurs when we have reached the starting point, i.e. the loop is closed.
In a digital image, each pixel has 8 surrounding neighbors. Location of the next pixel is specified by assigning discrete values from 1-8. The search for the location of the next pixel proceeds clockwise, i.e. search in the upper-left neighbor proceeds first before searching in the location directly above the seed, and so on. The next location becomes the new seed. These steps are repeated until the terminating condition is satisfied. This will effectively produce a vector. Because they are vectors, we can translate them, i.e. render them in another location just by plotting a pixel in the direction specified by its elements.
For further analysis, the curvatures of the shape are informative. These are obtained from the gradients (difference of two adjacent vectors) and running sums of three adjacent gradients. (More comments on gradients and running sums later)
 |
| Freeman vector code algorithm From: J.A.F. Balista et al. / Pattern Recognition Letters 31 (2010) 20–27 |
Prelude to chromosome classification
In this exercise we applied Freeman vector coding in analyzing a single chromosome pair. We begin with an image of a single chromosome pair. We first perform edge detection using a Sobel filter to produce the image on the right in the picture below
The resulting outline is thick. We can further tweak the intensity threshold or we can use a different filter. In our experiment we only used the outer boundary. We chose a pixel on the outer boundary as a starting point (x,y) = (2,49) and obtained the Freeman-vector code. A common problem we have encountered was when the algorithm failed to obtain the correct shape: algorithm did not terminate at the seed or a different shape is obtained. Even with the neighborhood search proceeding clockwise, the problem kept occurring.
Our solution was to incorporate a form of simple "memory" to the algorithm. This involved "remembering" and modifying the starting point of the neighborhood search. For pixels with codes 1-4, i.e. top half of the FVC, the search proceeds normally, with the neighborhood search still beginning at 1. For codes 5-8, the starting direction is 5, proceeding clockwise from 5 to 8, then 1 to 4. This can be done by a modulo operation or simply getting the overflow over 8.
Once we have obtained the correct shape, we compute for the gradients and running sums. To get two adjacent vectors, we obtain the difference between the original Freeman vector and the same vector shifted one element to the left. In the same manner, to get the running sum, we obtain the sum of the original gradient and two other, shifted once and twice to the left.
In the figure above, we obtained the FVC, and computed the gradients and running sum. We have labelled points of interest in all images. Our seed is at point H. It is interesting to note that the gradients indicates the slope of the curve at that point. It indicates the magnitude and direction of the change, i.e. increasing or decreasing. This seems to be the case for all points except C. Intuitively, and by inspection, the gradient should be more positive. What have we done wrong?
The fault is in our code.
From point B to C, the code is as string of 8's. Then at point C, we see it shifting in the direction of 1, Simply computing the gradient at that point results in a massive 1 - 8 = -7. We should probably modify the code to handle this but for now, we have left it as it is, and just made a mental note of it (likely a very bad practice in reality)
How do we find the chromosome's corners?
In the image of running sum, we see clumps of values (3 consecutive negative or positive values) about some points. At Point B, D, H and I, the cluster of values are positive (convex), including perhaps C, if we handled the case properly. While at points A, E, F, the values are negative (concave). These correspond very well to the corners in the image above. While at point G, there were no clustered values in the running sum, indicating that it is not a corner.
Dancing chromosomes
Two more processes are involved in chromosome classification: segmentation, axis and centromere
location, and classification. While we will not go into more detail about these processes, the location of the corners from the earlier algorithm may help us in this case. We compute for the center of our chromosome by taking the mean of the vertices. Prior to rotation, we translate them about about the origin at (0,0).
Rotation is done using the rotation matrix
This allows us to compute for the new location of the (x,y)
We can use a rotation angle based on the chromosome's axis, or in our case, the midpoint location between the top or bottom corners. In this demonstration, we deliberately chose to rotate it by -45 degrees. Results are shown in the image below. Incidentally, the location of the origin corresponds very well to the likeliest location of the centromere. Above the centromere are the short arms, and the below it are the long arms of the chromosome.
Summary
We have used the Freeman vector code to obtain a vector description of the chromosome's shapes. The gradient and the running sums of the adjacent vectors (generated) from the Freeman vector, allowed us to determine the location of chromosome's corners.
Additional Notes
- All algorithms were coded in R: Freeman vector coding, gradients, running sums, and rotation.
- The algorithm used in the original 1961 paper used the codes 0-7 and ran counter-clockwise.
- In the figure above of the Freeman vector code algorithm, we have not shown the color intensity patterns. See the paper for the complete image.
References
- H. Freeman (1961) ‘On the encoding of arbitrary geometric configurations’, IRE Trans. on Electronic Computers, 10(2):260-268
- J. Balista, M. Soriano, C. Saloma (2010) ‘Compact time-independent pattern representation of entire human gait cycle for tracking of gait irregularities’, Pattern Recognition Letters 31(1):20-27.
- Wikipedia contributors, "Shape," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Shape
- Wikipedia contributors, "Edge detection," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Edge_detection
- Wikipedia contributors, "Chromosome," Wikipedia, The Free Encyclopedia,https://en.wikipedia.org/wiki/Chromosome
- Soriano, M (2015), Image and Signal Feature Extraction: Shape, lecture notes distributed in Physics 301 - Special Topics in Experimental Physics (Advanced Signal and Image Processing) at National Institute of Physics, University of Philippines Diliman, Quezon City on 4 August 2015.


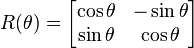


No comments:
Post a Comment